Artikel

Künstliche Intelligenz – Prognose von Hauspreisen

Beitrag von Christian Setzwein
17. November 2020

Schon seit ein paar Jahren ist der Kauf und Verkauf von Häusern ein Thema, das viele Menschen beschäftigt. Zugegebenermaßen auch mich, denn meine Frau und ich haben vor drei Jahren erst ein neues Haus gekauft und kurz danach unsere alte Immobilie veräußert. Wir haben beim Verkauf auf einen Makler verzichtet, und unsere größte Unsicherheit bestand darin, den Preis festzulegen. Diesem Problem haben sich jetzt vor allem Online-Makler Unternehmen angenommen, einige scheinen schottischer Abstammung zu sein, weil ihr Name mit einem großen M und einem kleinen c eingeleitet wird. Diese Firmen bieten an, unterstützt durch einen kleinen Online-Fragebogen, eine Prognose für den Preis des Hauses abzugeben.

Wie funktioniert das, wie kann eine Software lernen, derartige Prognosen zu erstellen? Ich möchte die Kernidee zunächst an einem stark vereinfachten Beispiel erläutern: Wir nehmen uns alle Zeitungen aus der Umgebung und notieren uns für alle Hausanzeigen in einer Tabelle die Werte „Quadratmeter Wohnfläche“ und „Preis“, etwas so:

Quadratmeter Wohnfläche	Preis in T€
108	379
75	185
116	496
150	545
103	394
140	445
64	197
180	559

Mit diesen Daten können wir jetzt unser Prognosemodell trainieren. Als Eingabe dient das Feature „Quadratmeter Wohnfläche“, als Zielwert (oder Label), der später für andere Datensätze prognostiziert werden soll, der Preis. In der Praxis würde man

mit viel mehr Datensätzen trainieren, um dem Algorithmus zu ermöglichen, Muster zu erkennen.
nicht nur mit einem Feature „Quadratmeter Wohnfläche“, sondern mit weiteren Features wie z.B „Anzahl Zimmer“, „Lage“, „Baujahr“ und weiteren trainieren. Die Auswahl der Features ist für die Güte der Prognose des Hauspreises entscheidend, man nennt diesen Vorgang das Feature-Engineering.

Doch weiter mit unserem einfachen Beispiel: Der Lernalgorithmus generiert nun für eine bestimmte Repräsentationsform (mathematische Funktion, Neuronales Netz), die wir ähnlich wie die Features auswählen, ein Prognosemodell. In unserem einfachen Beispiel entscheiden wir uns für eine lineare Funktion als Prognosemodell. Was der Lernalgorithmus macht, veranschaulicht die folgende Zeichnung:

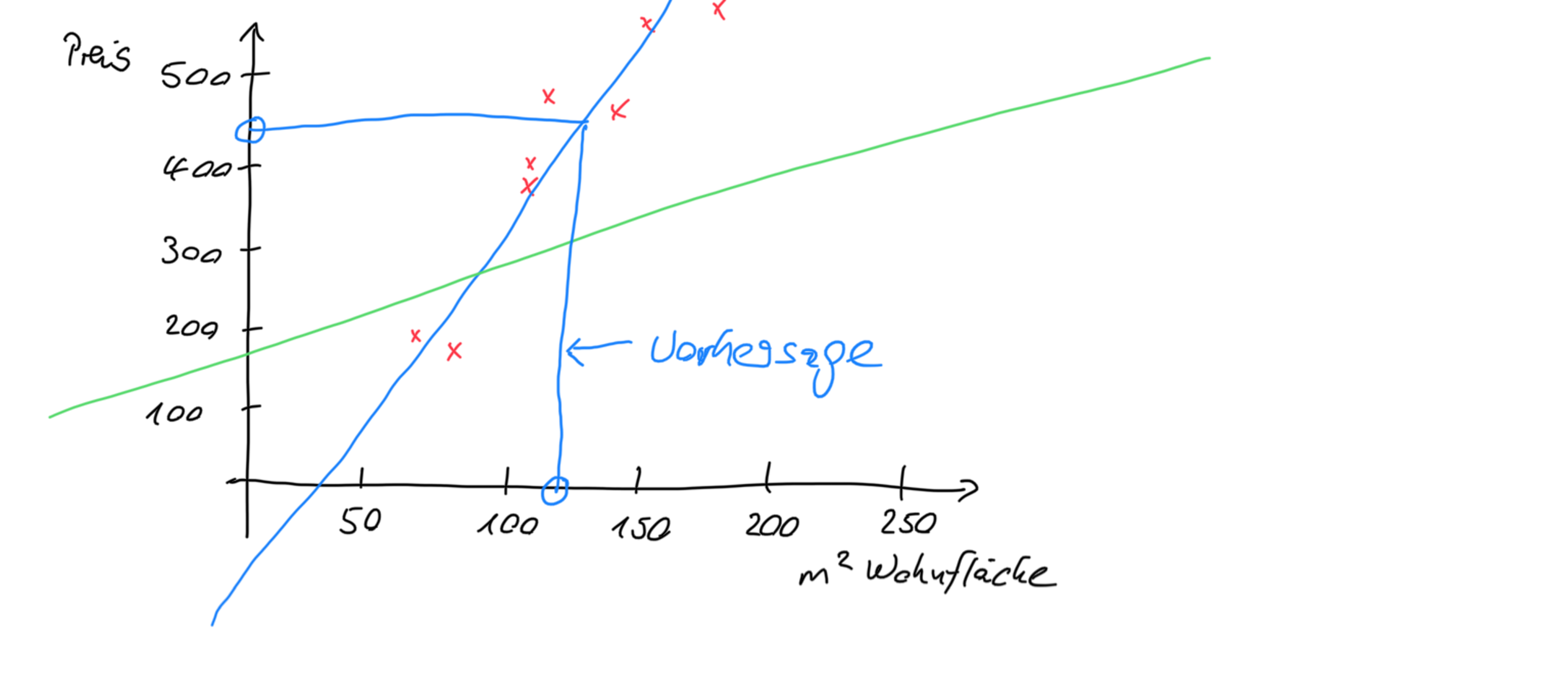
Der Lernalgorithmus generiert für die Trainingsdaten (die roten Kreuze) eine Gerade, die möglichst dicht an den Trainingsdaten liegt, hier die blaue Gerade. Er hätte auch die grüne Gerade generieren können, aber mit bloßem Auge sehen wir, das die blaue Gerade viel besser zu den Trainingsdaten passt. Unser einfaches Prognosemodell, wenn errechnet, ist nun fertig.

Wollen wir nun für ein beliebiges Haus den Preis prognostizieren, z.B. für ein Haus mit 120 qm (blauer Kreis auf der unteren Gerade), so lesen wir einfach auf der Gerade für den Preis den zugehörigen Wert ab, der durch unser Prognosemodell vorgegeben ist: ungefähr 420T€ (blauer Kreis auf der senkrechten Gerade).

Das Modell ist wie oben beschrieben wirklich stark vereinfacht, neben den oben genannten Punkten würde man in der Praxis auch eine komplexere Funktion verwenden (nicht nur eine Gerade), die sich besser an die Muster in den Trainingsdaten anpasst.

Das Finden der blauen Gerade durch die Software kann man sich anschaulich so vorstellen:

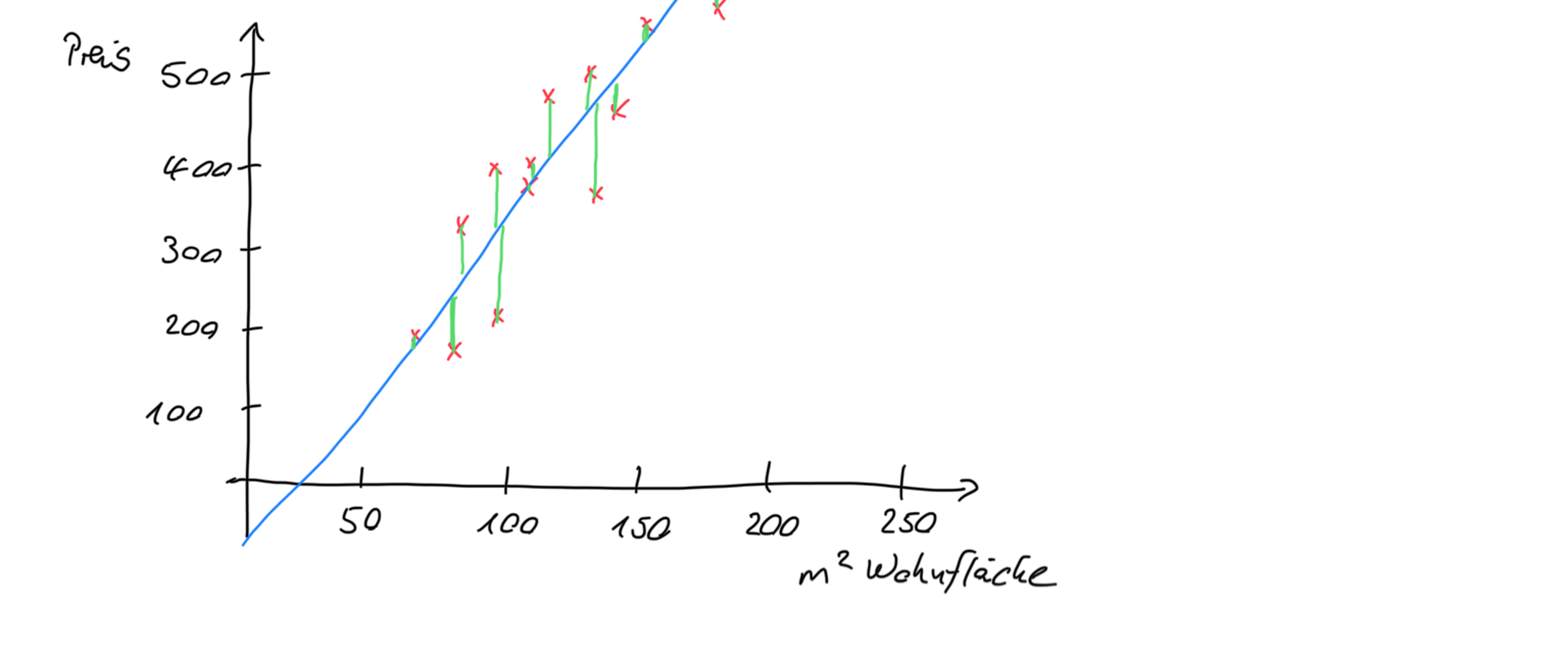
Der Lernalgorithmus prüft für unterschiedliche mögliche Geraden, wie weit der Wert aus dem Trainingsdatensatz (rotes Kreuz) von dem Wert entfernt ist, der durch die Gerade prognostiziert wird. In der obigen Grafik wird das durch die grünen Abstandhalter veranschaulicht. Die beste Gerade, die dann als Prognosemodell genommen wird, ist die, die diese Abstände zu den Trainingsdaten insgesamt für alle Trainingsdatensätze möglichst gering hält. Wen es noch tiefergehend interessiert: Mathematisch wird dies im Wesentlichen dadurch erreicht, dass man die Gerade sucht, deren Summe der Quadrate der Abweichungen am minimalsten ist.

Die vorgestellte Art des Lernens, um den Hauspreis vorherzusagen, nennt sich Supervised Learning. Die Software lernt, indem sie Beispiele bekommt (die roten Punkte), die in Zukunft von dem Prognosemodell als Antworten verlangt werden. Weil ein diskreter Wert, eine Zahl, prognostiziert werden soll, handelt es sich um ein sogenanntes Regressionsproblem, das durch die lernende Maschine gelöst wird.

Ich hoffe, Ihnen mit dem Beispiel „Prognose eines Hauspreises“ einen Einblick geliefert zu haben, wie Maschinen anhand von Trainingsdaten lernen und dann Prognosen liefern können. Um ein gutes Prognosemodell hinzubekommen, ist es jedoch nicht ganz so einfach wie in unserem Beispiel. Von den Herausforderungen beim Finden und Trainieren eines Modells werde ich in einem der vielen folgenden Artikel zur KI berichten. Jedem Supervised Learning Regressionsproblem liegen jedoch die vorgestellten Prinzipien, in Abwandlung und mit wachsender (mathematischer) Komplexität zugrunde.

Auch interessant:

Quelle Foto: @ Jeffrey Czum – Pexels.com

| Keine Kommentare